Blueberries and raspberries

In this post, I explain two common metrics used in the field of NLG (Natural Language Generation) and MT (Machine Translation).

BLUE score was first created to automatically evaluate machine translation, while ROUGE was created a little later inspired by BLUE to score a task of auto summurization. Both metrics are calculated using n-gram co-occurrence statistic and they both range from 0 to 1, 1 meaning sentences are exactly the same.

Despite their relative simplicity, BLEU and ROUGE similarity metrics are quite reliable since they were proven to highly correlate with human judgements.

One goal, two missions

Given two sentences, one written by human, being the reference / gold standard, and a second one generated by a computer, how automatically evaluate the similarity between them? BLEU and ROUGE try to answer this in two different contexts. BLEU for translation between two languages, and ROUGE for automatic summerization.

Here is an example of two similar sentences. We’ll use them in the following to illustrate the calculation of both metrics.

Type Sentence
Reference (by human) The way to make people trustworthy is to trust them.
Hypothesis/Canditate (by machine) To make people trustworthy, you need to trust them.

BLEU

BLEU score stands for Bilingual Evaluation Understudy.

When evaluating machine translation, multiple characterics are taken into account:

  • adequacy
  • fidelity
  • fluency

In its simplest form BLEU is the quotient of the matching words under the total count of words in hypothesis sentence (traduction). Regarding the denominator BLEU is a precision oriented metric.

\[p_n = { \sum_{n\text{-}gram \in hypothesis} Count_{match}(n\text{-}gram) \over \sum_{n\text{-}gram \in hypothesis} Count(n\text{-}gram) }= { \sum_{n\text{-}gram \in hypothesis} Count_{match}(n\text{-}gram) \over \ell_{hyp}^{n\text{-}gram} }\]

For example, the matches in the sample sentences are “to”, “make”, “people”, “trustworthy”, “to”, “trust”, “them”

Bleu score unigrams

\[p_1= { 7 \over 9 }\]

Unigram matches tend to measure adequacy while longer n-grams matches account for fluency.

Then precisions on various n-grams are aggregated using a weighted average of the logarithm of modified precisions.

\[BLEU_N = BP \cdot \exp{\left( \sum_{n=1}^N w_n \log p_n \right)}\]

To counter the disadvantages of precision metric, a breviety penality is added. Penality is none, i.e. 1.0, when the hypothesis sentence length is the same as the reference sentence length.

The brevity penality \(BP\) is function of the lengths of reference and hypothesis sentences.

\[BP = \left\{ \begin{array}{ll} 1 & \text{if } \ell_{hyp} \gt \ell_{ref} \\ e^{1 - { \ell_{ref} \over \ell_{hyp} }} & \text{if } \ell_{hyp} \le \ell_{ref} \end{array} \right.\]

BLEU example

Type Sentence Length
Reference The way to make people trustworthy is to trust them. \(\ell_{ref}^{unigram} = 10\)
Hypothesis To make people trustworthy, you need to trust them. \(\ell_{hyp}^{unigram} = 9\)

For this example we take parameters as the base line score, described in the paper, with \(N = 4\), and a uniform distribution, therefore taking \(w_n = { 1 \over 4 }\).

\[BLEU_{N=4} = BP \cdot \exp{\left( \sum_{n=1}^{N=4} { 1 \over 4 } \log p_n \right)}\]

We then calculate the precision \(p_n\) for the different n-grams.

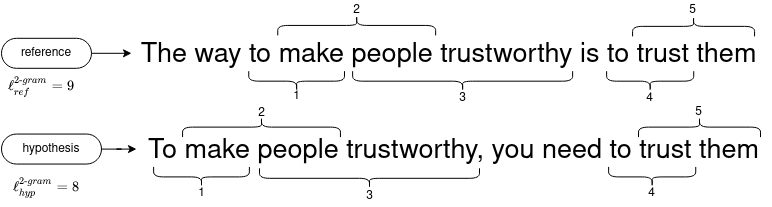
For instance, here is an illustration of the bigram (2-gram) matches Bleu score bigrams

The following table details the precisions for 4 n-grams.

n-gram 1-gram 2-gram 3-gram 4-gram
\(p_n\) \({ 7 \over 9 }\) \({ 5 \over 8 }\) \({ 3 \over 7 }\) \({ 1 \over 6 }\)

We then calculate the breviety penality \(BP = e^{1 - { \ell_{ref} \over \ell_{hyp} }} = e^{ - { 1 \over 9 }}\)

And finally we aggregate the precisions which gives:

\[BLEU_{N=4} \approx 0.33933\]

BLEU with python and sacreBLEU package

BLEU computation is made easy with the sacreBLEU python package.

For simplicity, the sentences are pre-normalized, removing punctuation and case folding

from sacrebleu.metrics import BLEU
bleu_scorer = BLEU()

hypothesis = "to make people trustworthy you need to trust them"
reference = "the way to make people trustworthy is to trust them"

score = bleu_scorer.sentence_score(
    hypothesis=hypothesis,
    references=[reference],
)

score.score/100 # sacreBLEU gives the score in percent

ROUGE

ROUGE score stands for Recall-Oriented Understudy for Gisting Evaluation.

Evaluation of summarization involves mesures of

  • coherence
  • conciseness
  • grammaticality
  • readability
  • content

In its simplest form ROUGE score is the quotient of the matching words under the total count of words in reference sentence (summurization). Regarding the denominator ROUGE is a recall oriented metric.

\[ROUGE_1 = { \sum_{unigram \in reference} Count_{match}(unigram) \over \sum_{unigram \in reference} Count(unigram) }= { \sum_{unigram \in reference} Count_{match}(unigram) \over \ell_{ref}^{unigram} }\]

ROUGE-1 example

ROUGE-1 is the ROUGE-N metric applied with unigrams.

Type Sentence Length
Reference The way to make people trustworthy is to trust them. \(\ell_{ref}^{unigram} = 10\)
Hypothesis To make people trustworthy, you need to trust them. \(\ell_{hyp}^{unigram} = 9\)

The following illustrates the computation of ROUGE-1 on the summurization sentences

Rouge-1 score unigrams

\[ROUGE_1= { 7 \over 10 } = 0.7\]

Four ROUGE metrics are defined is the ROUGE paper: ROUGE-N, ROUGE-L, ROUGE-W and ROUGE-S. The next section present the ROUGE-L score.

ROUGE-L

ROUGE-L or \(ROUGE_{LCS}\) is based on the length of the longest common subsequence (LCS). To counter the disadvantages of a pure recall metric as in ROUGE-N, Rouge-L calculates the weighted harmonic mean (or f-measure) combining the precision score and the recall score.

The advantages of \(ROUGE_{LCS}\) is that it does not require consecutive matches but in-sequence matches that reflect sentence level word order as n-grams. The other advantage is that it automatically includes longest in-sequence common n-grams, therefore no predefined n-gram length is necessary.

\[\left\{ \begin{array}{ll} R_{LCS} &= { LCS(reference, hypothesis) \over \ell_{ref}^{unigram} } \\ P_{LCS} &= { LCS(reference, hypothesis) \over \ell_{hypothesis}^{unigram} } \\ ROUGE_{LCS} &= { (1 + \beta^2) R_{LCS} P_{LCS} \over R_{LCS} + \beta^2 P_{LCS} } \end{array} \right.\]

ROUGE-L example

Rouge-L score

\[\left\{ \begin{array}{ll} R_{LCS} &= { 7 \over 10 } \\ P_{LCS} &= { 7 \over 9 } \\ ROUGE_{LCS} &= { (1 + \beta^2) 49 \over 70 + \beta^2 63 } \end{array} \right.\]

To give recall and precision equal weights we take \(\beta=1\)

\[ROUGE_{LCS}= { 98 \over 133 } \approx 0.73684\]

ROUGE with python and Rouge package

ROUGE computation is made easy with the Rouge python package.

For simplicity, sentences are pre-normalized, removing punctuation and case folding

from rouge import Rouge
rouge_scorer = Rouge()

hypothesis = "to make people trustworthy you need to trust them"
reference = "the way to make people trustworthy is to trust them"

score = rouge_scorer.get_scores(
    hyps=hypothesis,
    refs=reference,
)
score[0]["rouge-l"]["f"]

BLEU VS ROUGE

A short summary of the similitudes of the two scoring methods:

  • Inexpensive automatic evaluation
  • Count the number of overlapping units such as n-gram, word sequences, and word pairs between hypothesis and references
  • The more reference sentences the better
  • Correlates highly with human evaluation
  • Rely on tokenization and word filtering, text normalization
  • Does not cater for different words that have the same meaning — as it measures syntactical matches rather than semantics

And here is for the differences:

BLEU score ROUGE score
Initially made for translation evaluations (Bilingual Evaluation Understudy) Initially made for summary evaluations (Recall-Oriented Understudy for Gisting Evaluation)
Precision oriented score Recall oriented score, in this ROUGE-N version
One version Multiple versions

Sources