Rose apples a.k.a. bell fruits

This post is just about simple ARIMA processes, some common notations and functions in time series analysis.

Table of contents

General notations

ARIMA processes can be expressed with a parametric equation:

\[z_t' = \phi_0 + \sum^p_{i=1}\phi_i z'_{t-i} + \epsilon_t + \sum^q_{i=1}\theta_i\epsilon_{t-i}\] \[z_t' = \phi_0 + \phi_1 z'_{t-1} + \phi_2 z'_{t-2} + ... + \phi_p z'_{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + ... + \theta_q \epsilon_{t-q}\]

where

  • \(z_t'\) is the \(z_t\) variable after \(d^{th}\) differentiations
  • \(\epsilon_t \sim N(0,1)\) is gaussian white noise with zero mean and unit variance
  • \(p,d,q\) are integers
  • \(\{ \phi_i \}\) and \(\{ \theta_i \}\) are model parameters, all reals

ARIMA processes can also be expressed with the help of a backward shift operator:

\[\Phi_p(B)(1 - B)^dz_t = \Theta_q(B)\epsilon_t\]

where

  • \(B\) is the backward shift operator defined as \(Bz_t = z_{t-1}\), and more generally for \(k \in \mathbb{N}^+\)
\[B^kz_t = z_{t-k}\]

  • \(\Phi_p\) is a polynomial in \(B\) such as \(\Phi_p(B) = 1 -\phi_1B - \cdots - \phi_pB^p\)

  • and \(\Theta_q\) is a polynomial in \(B\) with \(\Theta_q(B) = 1 + \theta_1B + \cdots + \theta_qB^q\)

Can also be written with the gradient (\(\nabla\)) operator:

\[\Phi_p(B)\nabla^dz_t = \Theta_q(B)\epsilon_t\]

Codependencies

A correlation of a variable with itself at different times is known as autocorrelation. When a value \(Z_t\) is correlated with a subsequent value \(Z_{t+h}\) at lag \(h\) then autocovariance function can be expressed as:

\[Cov(Z_t, Z_{t+h}) = \gamma_Z(h) = E[(Z_t - \mu_t)(Z_{t+h} - \mu_{t+h})]\]

If a time series model is second-order stationary, which means stationary in both mean and variance, \(\forall t\): \(\mu_t = \mu\) and \(\sigma_t = \sigma\), then:

\[Cov(Z_t, Z_{t+h}) = \gamma_Z(h) = E[(Z_t - \mu)(Z_{t+h} - \mu)]\]

Autocorrelation function is defined as:

\[ACF(Z_t, Z_{t+h}) = \rho_Z(h) = { Cov(Z_t, Z_{t+h}) \over \sqrt{ Var(Z_t) Var(Z_{t+h}) } } = { \gamma_Z(h) \over \gamma_Z(0) } = { \gamma_Z(h) \over \sigma^2 }\]

The partial autocorrelation function (PACF) at lag \(h\) shows the autocorrelation between \(Z_t\) and \(Z_{t+h}\) after the dependencies of \(Z_t\) on \(Z_{t+1} \cdots Z_{t+h-1}\) have been removed.

It can be shown that the PACF is the correlation between the prediction errors \(Z_t - \hat{Z}_t\) and \(Z_{t+h} - \hat{Z}_{t+h}\):

\[PACF(Z_t, Z_{t+h}) = \alpha_Z(h) = Cor(Z_t - \hat{Z}_t, Z_{t+h}-\hat{Z}_{t+h})\]

PACF is sensitive to outliers

Simple zero-mean and unit-variance models

In this section we observe simple zero-mean models, where \(\phi_0\) and \(\theta_0\) are equal to zero. We also take \(\{ \epsilon_t \} \sim N(\mu=0,\sigma^2=1)\). The following table shows the models we’ll analyze.

Instantiation ARIMA(p,d,q)
Gaussian White Noise ARIMA(0,0,0)
Gaussian Random Walk ARIMA(0,1,0)
First-Order Linear Autoregression ARIMA(1,0,0)
First-Order Moving Average ARIMA(0,0,1)

Gaussian White Noise - ARIMA(0,0,0)

A white noise process is the special case of an ARIMA process when \(p= d =q =0\).

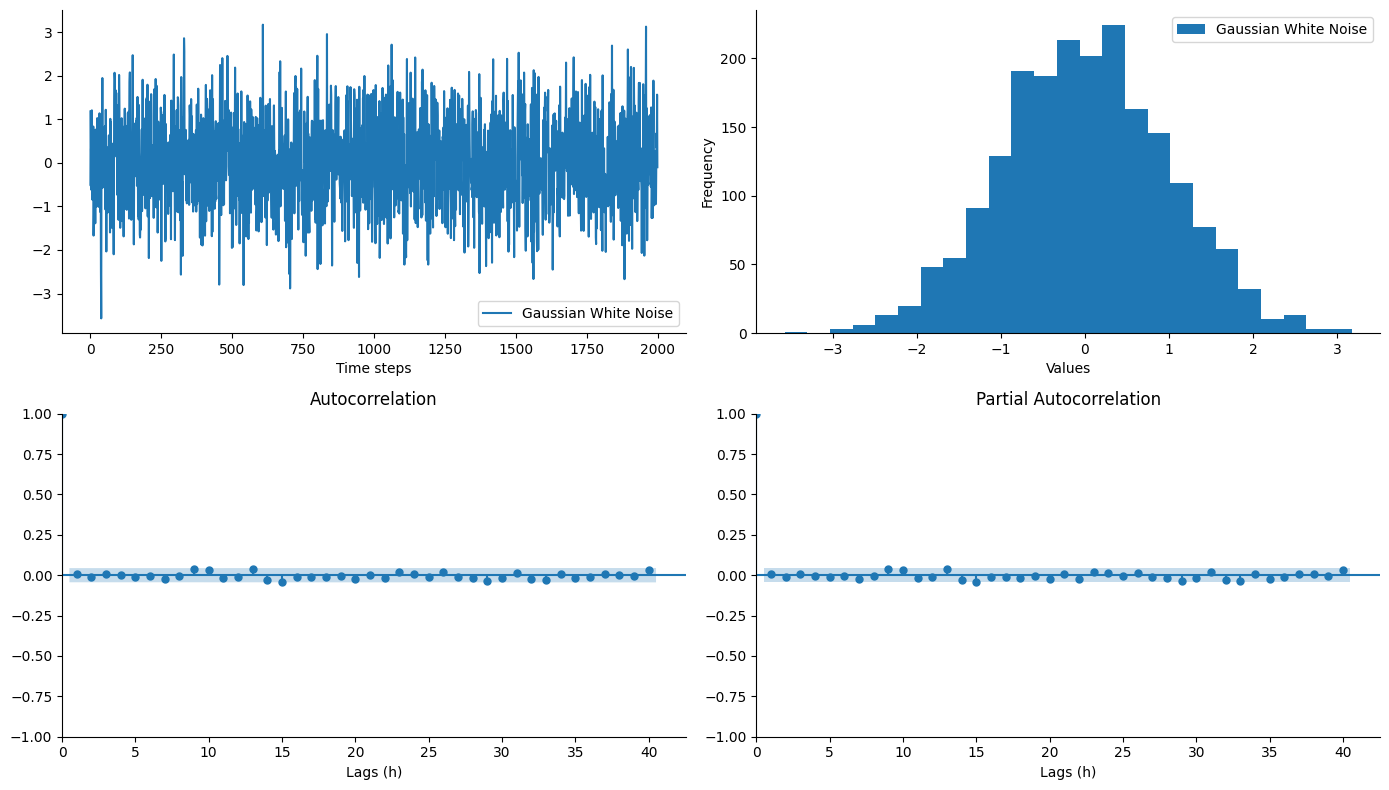
Gaussian White Noise Process

Parametric Notation Backward Shift Notation
\(z_t = \epsilon_t\) \(\Phi_0(B)(1 - B)^0 z_t = \Theta_0(B)\epsilon_t\)
Autocovariance ACVF Autocorrelation ACF Partial Autocorrelation PACF
\(\gamma_{z}(t + h, t) = \left\{ \begin{array}{ll} 1, & \text{if } h = 0 \\ 0, & \text{if } h \ne 0 \end{array} \right.\) \(\rho_{z}(h) = \left\{ \begin{array}{ll} 1, & \text{if } h = 0 \\ 0, & \text{if } h \ne 0 \end{array} \right.\) \(\alpha_{z}(h) = \left\{ \begin{array}{ll} 1, & \text{if } h = 0 \\ 0, & \text{if } h \ne 0 \end{array} \right.\)

Gaussian Random Walk - ARIMA(0,1,0) - I(1)

A random walk process is the special case of an ARIMA process when \(p=q =0\) and \(d=1\).

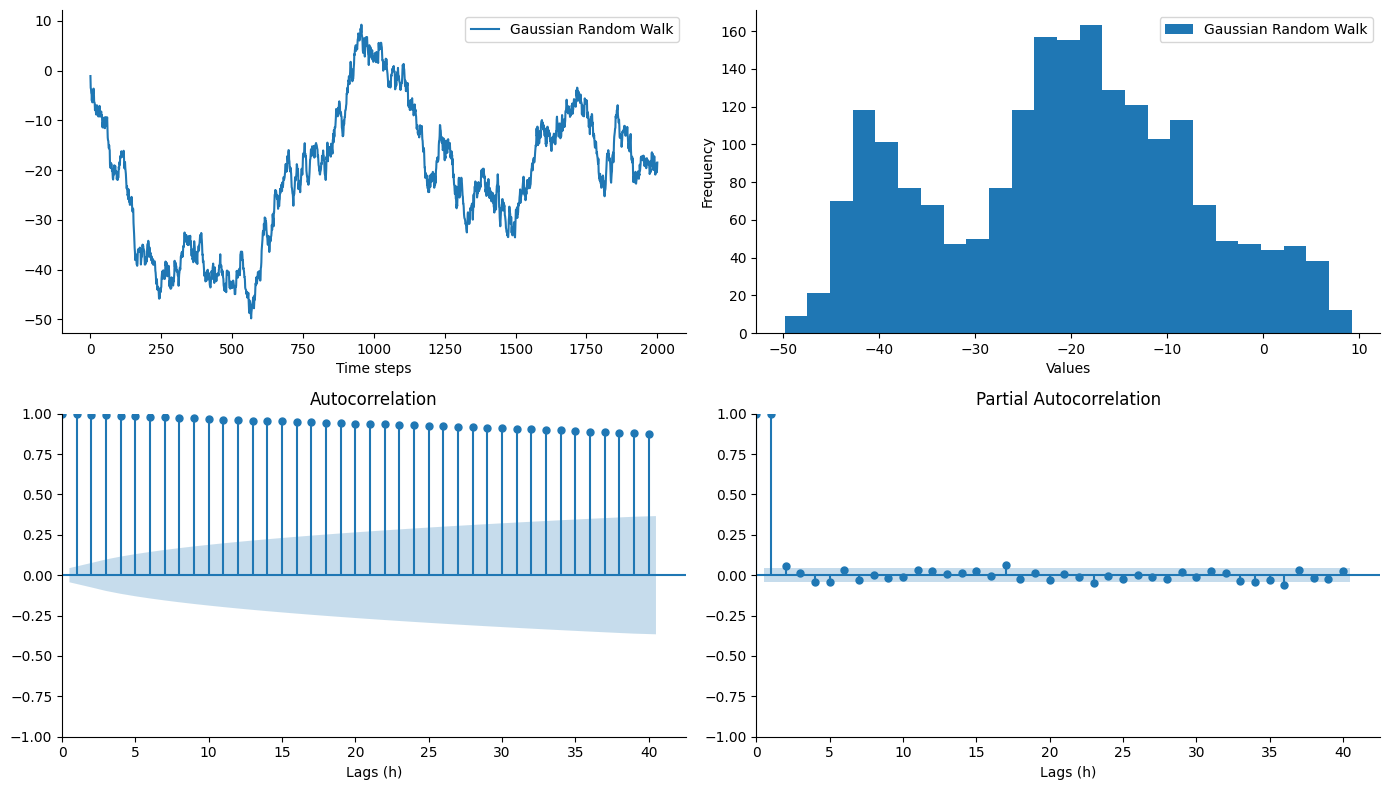
Gaussian Random Walk Process

Parametric Notation Backward Shift Notation
\(z_{t} = z_{t-1} + \epsilon_t\) \(\Phi_0(B)(1 - B)^1 z_t = \Theta_0(B)\epsilon_t\)
Autocovariance ACVF Autocorrelation ACF Partial Autocorrelation PACF
\(\gamma_{z}(t + h, t) = t\) \(\rho_{z}(h) = 1\) \(\alpha_z(h) = \left \{ \begin{array}{ll} 1, & \text{if } h \le 1 \\ 0, & \text{if } h \gt 1 \end{array} \right.\)

First-Order Linear Autoregression - ARIMA(1,0,0) - AR(1)

A first-order autoregressive process is the special case of an ARIMA process when \(p=1\) and \(d=q=0\).

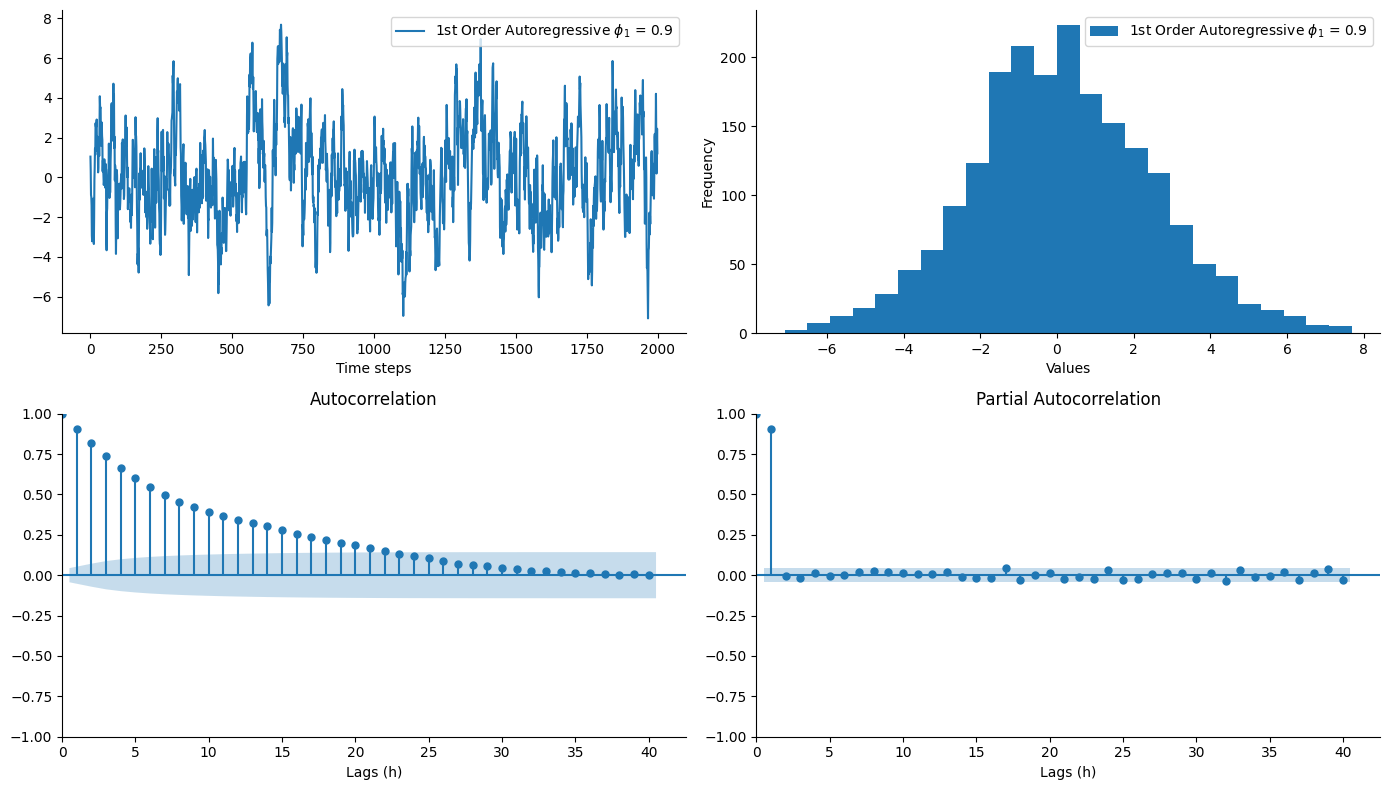
First-Order Autoregressive Process

Parametric Notation Backward Shift Notation
\(z_t = \phi_0 + \sum^p_{i=1} \phi_i z_{t-i} + \epsilon_t\) \(\Phi_1(B)(1 - B)^0 z_t = \Theta_0(B)\epsilon_t\)
\(z_t = \phi_1 z_{t-1} + \epsilon_t\) \((1 -\phi_1B) z_t = \epsilon_t\)
Autocovariance ACVF Autocorrelation ACF Partial Autocorrelation PACF
\(\gamma_{z}(h) = {\phi_1}^h \gamma_{z}(0)\) \(\rho_{z}(h) = {\phi_1}^{\lvert h \rvert}\) \(\alpha_z(h) = \left \{ \begin{array}{ll} 1, & \text{if } h = 0 \\ {\phi_1}^2, & \text{if } h = 1 \\ 0, & \text{if } h \gt 1 \end{array} \right.\)

First-Order Moving Average - ARIMA(0,0,1) - MA(1)

A first-order moving average process is the special case of an ARIMA process when \(p=d=0\) and \(q=1\).

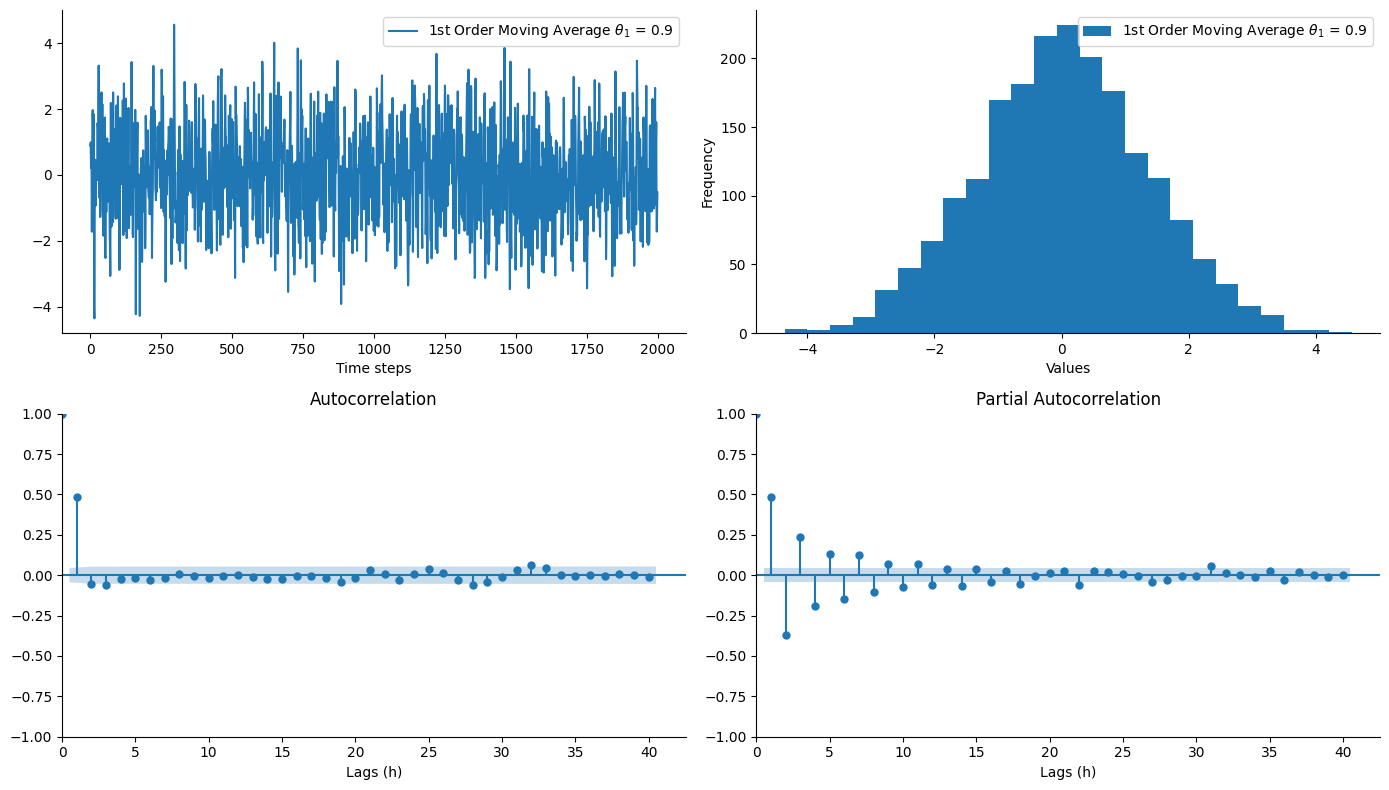
First-Order Moving Average Process

Parametric Notation Backward Shift Notation
\(z_t = \theta_0 + \sum^q_{i=1} \theta_i \epsilon_{t-i} + \epsilon_t\) \(\Phi_0(B)(1 - B)^0 z_t = \Theta_1(B)\epsilon_t\)
\(z_t = \theta_1 \epsilon_{t-1} + \epsilon_t\) \(z_t = (1 + \theta_1B)\epsilon_t\)
Autocovariance ACVF Autocorrelation ACF Partial Autocorrelation PACF
\(\gamma_{z}(h) = \left\{ \begin{array}{ll} 1 + \theta_1^2, & \text{if } h = 0 \\ \theta_1, & \text{if } h = \pm 1 \\ 0, & \text{if } \lvert h \rvert \gt 1 \end{array} \right.\) \(\rho_{z}(h) = \left\{ \begin{array}{ll} 1, & \text{if } h = 0 \\ \theta_1^2, & \text{if } h = \pm 1 \\ 0, & \text{if } \lvert h \rvert \gt 1 \end{array} \right.\) \(\alpha_z(h) = \left \{ \begin{array}{ll} 1, & \text{if } h = 0 \\ { -(- \theta_1)^h \over 1 + \theta_1^2 + \cdots + \theta_1^{2h} }, & \text{if } h \gt 0 \end{array} \right.\)

Sources